Геофизики увидели приливные деформации породы с помощью сейсмических волн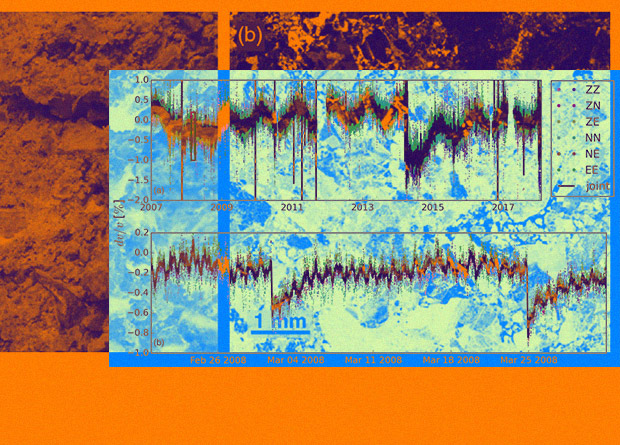

Геофизики из Германии придумали способ, с помощью которого можно точно измерять колебания скорости сейсмических волн, связанные с деформациями породы. В частности, ученым удалось соотнести колебания скорости с приливными силами. При этом ученые не создавали сейсмические волны искусственно и полагались на данные только одной сейсмологической станции. Статья опубликована в Physical Review Letters, кратко о ней сообщает Physics.

Как правило, геологические породы неоднородны, а потому их эластические свойства существенно зависят от величины приложенной силы. Теоретически это позволяет оценить напряженность породы с помощью сейсмических волн, скорость которых напрямую связана с эластическими свойствами породы. Такие оценки необходимы при разработке шахт и строительстве; кроме того, с их помощью можно наблюдать за геологическими процессами в окрестности вулканов и геологических разломов. К сожалению, установить, как скорость сейсмических волн связана с напряженностью конкретной породы, очень сложно. Конечно, такую зависимость можно получить в лаборатории, точно контролируя состав и напряженность породы, однако перенести этот результат на реальные системы, состав которых неизвестен, а сила воздействия неконтролируема, практически невозможно из-за высокой погрешности данных. Поэтому ученым приходится разрабатывать альтернативные методы, с помощью которых эластические свойства породы можно измерить непосредственно.

В основном, такие методы делятся на две группы. С одной стороны, можно устроить контролируемый взрыв и измерить параметры родившихся сейсмических волн. Этот метод позволяет получить довольно точные результаты, однако из-за высокой стоимости и сложности ученые редко к нему прибегают. С другой стороны, можно отслеживать природные события и корреляции между деформациями пород и природным шумом с помощью тысяч сейсмологических станций, расположенных по всему миру. Этот способ сравнительно дешев, однако его точность не позволяет сделать каких-либо значимых заключений. До сих пор ученым удавалось, в лучшем случае, различить периоды повышенной и пониженной напряженности пород, связанные с приливными силами (то есть притяжением Луны).

Геофизики Кристоф Сенс-Шёнфельдер (Christoph Sens-Sch?nfelder) и Том Ойленфельд (Tom Eulenfeld) придумали, как измерить эластические свойства породы точно, быстро и дешево. Ученые использовали автокорреляционную технику, чтобы получить эхо-импульсную корреляционную функцию (pulse-echo Green’s function). Другими словами, физики записывали сейсмический сигнал одной-единственной станции и искали в нем следы сейсмических волн, которые прошли через детектор, отразились от породы и вернулись к нему обратно.

Для наблюдений ученые выбрали станцию Патаче (PATCX — Patache), которая находится в пустыне Атакама в северной части Чили. Эта станция отслеживает изменения скорости сейсмических волн, связанные как с землетрясениями, так и с тепловыми деформациями окружающих ее пород. В основном порода в окрестности станции представляет собой «гипсобетонную» матрицу (gypcrete), в которую включены многочисленные обломки эвапоритов (гипса или галита). Физики собирали данные ровно двенадцать лет, с 1 января 2007 и по 31 декабря 2018. Относительная погрешность измерений при этом не превышала одной тысячной процента.

Несмотря на то, что приливные силы Луны сравнительно невелики, они вызывают ряд интересных эффектов (помимо приливов, очевидно). Например, в 2014 году американские климатологи с помощью спутников обнаружили колебания атмосферного давления, связанные с лунной гравитацией: когда Луна находится у вас над головой или прямо под ногами, атмосферное давление повышается. Более того, два года спустя ученые показали, что от этих колебаний зависит уровень осадков в тропиках. В 2016 году японские сейсмологи показали, что приливные силы могут быть связаны с катастрофическими землетрясениями: наиболее сильные и разрушительные землетрясения происходят во время полнолуния и новолуния. Для этого ученые проанализировали данные о десяти тысячах землетрясениях, произошедших за последние двадцать лет. А в 2017 году физики использовали приливные силы для проверки теории, которая могла бы объединить Стандартную модель и Общую теорию относительности. Если бы эта модель была верна, лунная гравитация нарушала бы лоренц-инвариантность уравнений движения.

Дмитрий Трунин

Источник: nplus1.ru